[教育講演]
複雑系の科学と医学
| 松戸隆之 |
| 新潟大学医学部検査診断学 |
はじめに
複雑系の科学は、自然界の複雑な現象を解析するために、主として物理学、数学の分野で発展してきた概念、理論を発展させ、自然に対する新しい視点を確立しようとする科学の新しい潮流である。その対象は乱流、気象から社会現象、進化におよび、最大のターゲットとして生体と脳がある[1][2]。デカルト以来の近代科学は、対象をその格成要素に分解し、個々の要素の性質を解明して、それらを重ね合わせることにより全体を理解しようとしてきた。要素還元論と呼ばれるこの科学の基本戦略はさまざまな分野で大きな成功をおさめ、医学、生物学領域でも、生体の究極の構成要素である遺伝子の全構造の解明が遠からず実現されようとしている。ヒトゲノム計画の完成により、生体の物質的基盤の全貌が明らかになったとき、われわれは生体を支配している原理のすべてを手にすることができるのであろうか。生体を含む自然界では、さまざまな構成要素が相互作用を及ぼし合いながら共存している。しかもこの相互作用は、多くの場合非線形性(入力と出力が単純に比例しないような関係)を示す。非線形性を含む系では重ね合わせの原理は成立せず、カオスの項で述べるような不思議な現象が現れる。
複雑系の科学は要素還元論とは逆に、構成要素の相互作用から、より高次の実体としての全体が形成されるしくみ、混沌から秩序が自律的に生ずる、自然の自己組織性の原理を解明することを究極の目的としている。
本稿では複雑系の科学の基礎概念の一部としてフラクタルとカオスを紹介し、医学におけるその意義について考察する。
フラクタル
フラクタル(fractal)とは自己相似性をもつ構造のことをいう。Fig.1はSielpinskie gasketと呼ばれる図形で、この図形は三角形の中央を無限にくりぬいてゆくという操作によって得られる。全体を構成する3つの部分は、全体を1/2に縮小した完全なコピーとなっており、この図形は2次元的な広がりをもちながらその面積は0である。このような図形の特徴を表現する指標としてフラクタル次元というものが考えられた。直線や長方形などの通常の図形は全体の中にそれ自身を1/aに縮小した図形をb=aD個含む(直線ではD=1、長方形ではD=2)。従って次元Dをlogabと定義すると、Sielpinskie gasketではD=log23=1.5849...という非整数の次元が得られる。このように非整数次元をもつ図形をフラクタルとよぶ。

自然界ではSielpinskie gasketのように厳密な自己相似性をもつ図形は存在しないが、雲、海岸線、地形の凹凸、樹木の枝の分岐などでは、一部分を拡大すると全体とよく似た構造が認められる。このように部分が全体によく似ているという性質をも取り扱えるように次元の定義を拡張すると(Hausdorff次元、相関次元など)、雲では2.3、樹木の枝では1.5というように非整数の次元が得られる。生体にも気管支、血管系、神経の樹状突起など、後者の意味でフラクタル性を示す構造が多数認められる[3]。
カオス
カオスとは決定論的な法則により引き起こされる複雑で、不規則かつ不安定な振る舞いをさす。辞書的にはchaosは混沌と訳されるが、複雑系の科学におけるカオスは決定論的な法則に支配されているという点が本質的な特徴であり、この意味でdeterministic chaosとも呼ばれる。カオスの性質を説明するために、昆虫などの個体数の変動をモデル化したlogistic mapの例を示す[4]。logistic mapは
xn+1=axn(1-xn)
と表現される離散写像で、xnは今年の個体数(0〜l)、xn+1は翌年の個体数、aは繁殖力を表す。
xnの時間的発展はaとxの初期値x0を与えれば厳密に決定される。aが3より小さいときにはxnは一つの値に収束してゆく。しかしaが3を超えるとxnは2つの値の間で振動するようになり、さらにaを増加させると4周期、8周期、16周期点が次々と現れ(周期倍化現象)、a=3.5699...以上でカオスとなる。Fig.2はa=4(pure chaos)の状態を示したものであり、ここではxnの値は0から1の間を乱雑に動き回り周期性は認められない。
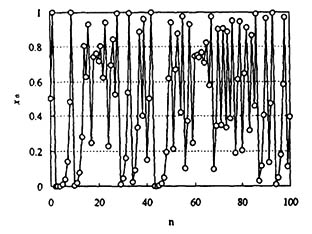
カオスでは初期値がわずかに異なる場合、その違いが指数関数的に増福されて、まったく異なる経過をたどるようになる(初期値敏感性)。現実の系では観測誤差のため初期値を厳密に決定することはできないから、もし系を支配する法則が厳密に分かっていても、カオスでは長期的な予測は不可能となる。
系の時間的変化を、系の状態を表す空間(相空間)点列としてプロットすると一つの軌道(trajectory)が得られる。系がどのような状態から始まっても一つの安定状態に向かって変化する場合には軌道は一つの点に巻き込まれる(安定平衡点)。また周期的な変動が安定となる場合は軌道は一つの閉曲線に引き込まれる(limit cycle)。このように軌道を引き込む構造を attractorと呼ぶが、カオスではFig.3のような妙なattractor が現れ(strange attractor)、この attractorはフラクタル性を示す。
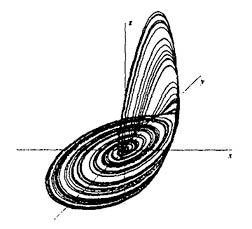
複雑系の科学と医学
フラクタル次元は自己相似性を示す構造の特徴を定量的に与える指標であるが、この意味でさまざまな生体構造、現象のフラクタル次元が計算されている。また次元を局所的に計算することにより、細胞配列のパターンからの癌の検出も試みられている。一方、フラクタルの考え方は、簡単な規則から複雑な構造を生成する手順を与える。遺伝子は生体の全構造を記述するには情報量が少なすぎることが知られているが、遺伝子は生体を構成するためのルールの集合で、スケールを変えてこのルールを適用することにより複雑な構造を生成しているとも考えられる。カオスでは比較的簡単な法則が不規則で複雑な変動を引き起こす。生体では一見不規則な変動が無数に存在するが、これらはノイズの混入ではなく、カオス、すなわち厳密な法則の存在を示しているのかもしれない。
Logistic mapの例でも示した通り、ある系に、ある量を増やそうとする力と減らそうとする力とが働くとき、系の状態は一つの安定状態に収束するとは限らない。この意味で、生理学の基本原理であるホメオスタシスの概念は根本的な見直しが必要であると思われる。
生体では神経細胞の興奮膜について、カオスの存在が理論的、実験的に証明されている[5]。さらに心筋細胞、脳波、心拍変動、脈波、ホルモン分泌などで、カオスの存在を示唆する所見が報告されている。
Goldberger 等は心拍数変動の解析から、健常者ではカオス的変動が認められ、心不全や突然死を起こした患者の心拍数では周期的変動や変動の減少が認められたことを報告している[3]。この事実は生体がカオスを積極的に利用している可能性を示唆する。またSchiff等はカオス理論に基づく制御技術により、海馬のスライスの神経回路網で、周期的あるいはカオス的電位変動の発生を自由にコントロールできることを示した[6]。これらの発見は、臨床医学においても、カオス理論を含む複雑系の科学の解析手法が有用であることを示唆し、また疾患の治療においても従来とは全く異なる観点からのアプローチが可能であることを示している。
【参考文献】
- 1.
- 金子邦彦、津田一郎:複雑系のカオス的シナリオ,朝倉書店.1996.
- 2.
- I.プリゴジン,I.スタンジェール:混沌からの秩序,みすず書房.1987.
- 3.
- A.L.ゴールドバーガー他:身体の中のカオスとフラクタル,日経サイエンス4月号,57-65,日経サイエンス社,1990.
- 4.
- May, R.M. :Simple mathematical models with very complicated dynamics,Nature,261,459-67,1976.
- 5.
- 合原一幸編著:カオス−カオス理論の基礎と応用一.サイエンス社.1990.
- 6.
- Schiff, S.J. et al:Controllin chaos in the brain,Nature,370,615−620,1994.